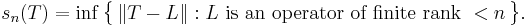Singular value
In mathematics, in particular functional analysis, the singular values, or s-numbers of a compact operator T : X → Y acting between Hilbert spaces X and Y, are the square roots of the eigenvalues of the nonnegative self-adjoint operator T*T : X → X (where T* denotes the adjoint of T).
The singular values are nonnegative real numbers, usually listed in decreasing order (s1(T), s2(T), …). If T is self-adjoint, then the largest singular value s1(T) is equal to the operator norm of T (see Courant minimax principle).
In the case that T acts on euclidean space Rn, there is a simple geometric interpretation for the singular values: Consider the image by T of the unit sphere; this is an ellipsoid, and its semi-axes are the singular values of T (the figure provides an example in R2).
In the case of a normal matrix A, the spectral theorem can be applied to obtain unitary diagonalization of A as per A = UΛU*. Therefore,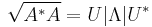 
and so the singular values are simply the absolute values of the eigenvalues.
Most norms on Hilbert space operators studied are defined using s-numbers. For example, the Ky Fan-k-norm is the sum of first k singular values, the trace norm is the sum of all singular values, and the Schatten norm is the pth root of the sum of the pth powers of the singular values. Note that each norm is defined only on a special class of operators, hence s-numbers are useful in classifying different operators.
In the finite-dimensional case, a matrix can always be decomposed in the form UDW, where U and W are unitary matrices and D is a diagonal matrix with the singular values lying on the diagonal. This is the singular value decomposition.
History
This concept was introduced by Erhard Schmidt in 1907. Schmidt called singular values "eigenvalues" at that time. The name "singular value" was first quoted by Smithies in 1937. In 1957, Allakhverdiev proved the following characterization of the nth s-number:
This formulation made it possible to extend the notion of s-numbers to operators in Banach space.